Gender Discrimination

Relationship Salary - Gender ?

The data frame omega contains the salaries for the sample of 50 executives in the company. Can you conclude that there is a significant difference between the salaries of the male and female executives?

Note that you can perform different types of analyses, and check whether they all lead to the same conclusion

. Confidence intervals . Hypothesis testing . Correlation analysis . Regression

Calculate summary statistics on salary by gender. Also, create and print a dataframe where, for each gender, you show the mean, SD, sample size, the t-critical, the SE, the margin of error, and the low/high endpoints of a 95% condifence interval

# Summary Statistics of salary by gender
df_by_gender<-mosaic::favstats (salary ~ gender, data=omega)

# Dataframe with two rows (male-female) and having as columns gender, mean, SD, sample size, 
# the t-critical value, the standard error, the margin of error, 
# and the low/high endpoints of a 95% confidence interval

df_by_gender2<- df_by_gender %>% 
  mutate(t_critical=qt(.975,n-1), standard_error=sd/sqrt(n), upper_95=mean+t_critical*standard_error, lower_95=mean-t_critical*standard_error) %>% select(gender,mean,sd,n,t_critical,standard_error,upper_95,lower_95)

df_by_gender2

##   gender  mean   sd  n t_critical standard_error upper_95 lower_95
## 1 female 64543 7567 26       2.06           1484    67599    61486
## 2   male 73239 7463 24       2.07           1523    76390    70088

# We can see that the confidence intervals for men and women in regards to salary do not overlap. This would allow us to reject the null hypothesis, but we will carry out hypothesis testing anyway and analyse the relationships between all the remaining factors.

#We will draw a scatterplot to visually inspect relationship between salary and experience

ggplot(df_by_gender,aes(x=gender,y=mean, colour= gender,fill=gender)) +
  geom_col() +
  labs(title = "On Average Male Executives Make More at Omega", x="", y= "Salary (in USD)") +
  theme_bw()+
  scale_y_continuous(labels= scales::dollar)+
  theme(legend.position = "none")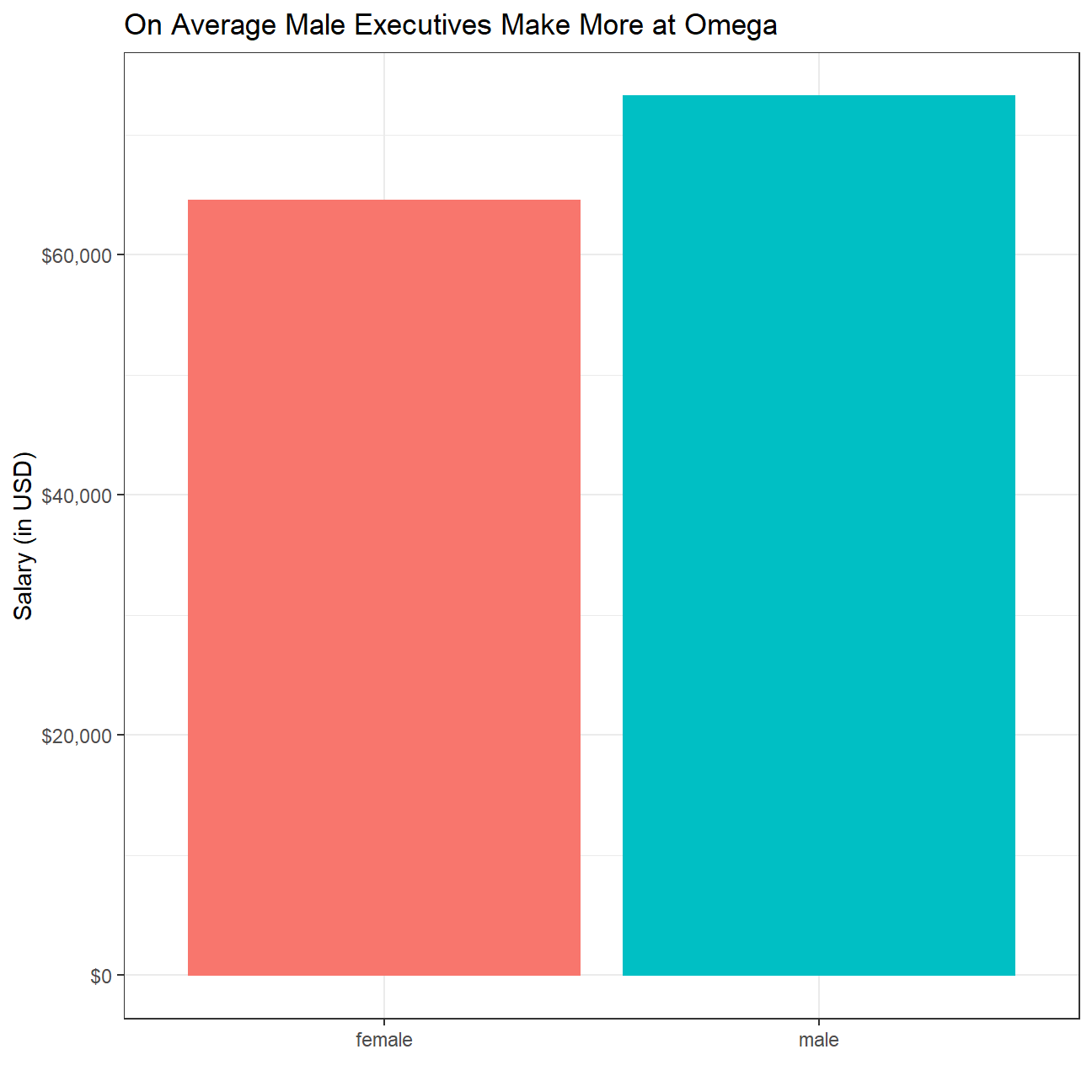

We can observe a strong relationship between salary and experience. Increase in salary comes quickly at the beginning and throughout the first ~15 years, however the gains in salary become slower later over time, displaying diminishing marginal returns.

We will further investigate the difference between salaries by gender through hypothesis testing, utilizing both t.test() and the simulation method from the infer package.

# hypothesis testing using t.test() 
t.test(salary~gender, data=omega)

## 
##  Welch Two Sample t-test
## 
## data:  salary by gender
## t = -4, df = 48, p-value = 2e-04
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -12973  -4420
## sample estimates:
## mean in group female   mean in group male 
##                64543                73239

# hypothesis testing using infer package
set.seed(12345)
salary_by_gender<- omega %>% 
  specify(salary~gender) %>% 
  hypothesize(null="independence") %>% 
  generate(reps=1000,type="permute") %>% 
  calculate(stat="diff in means",
            order=c("male","female"))

salary_by_gender %>% visualize()+shade_p_value(obs_stat = df_by_gender2[2,2]-df_by_gender2[1,2], direction = "both")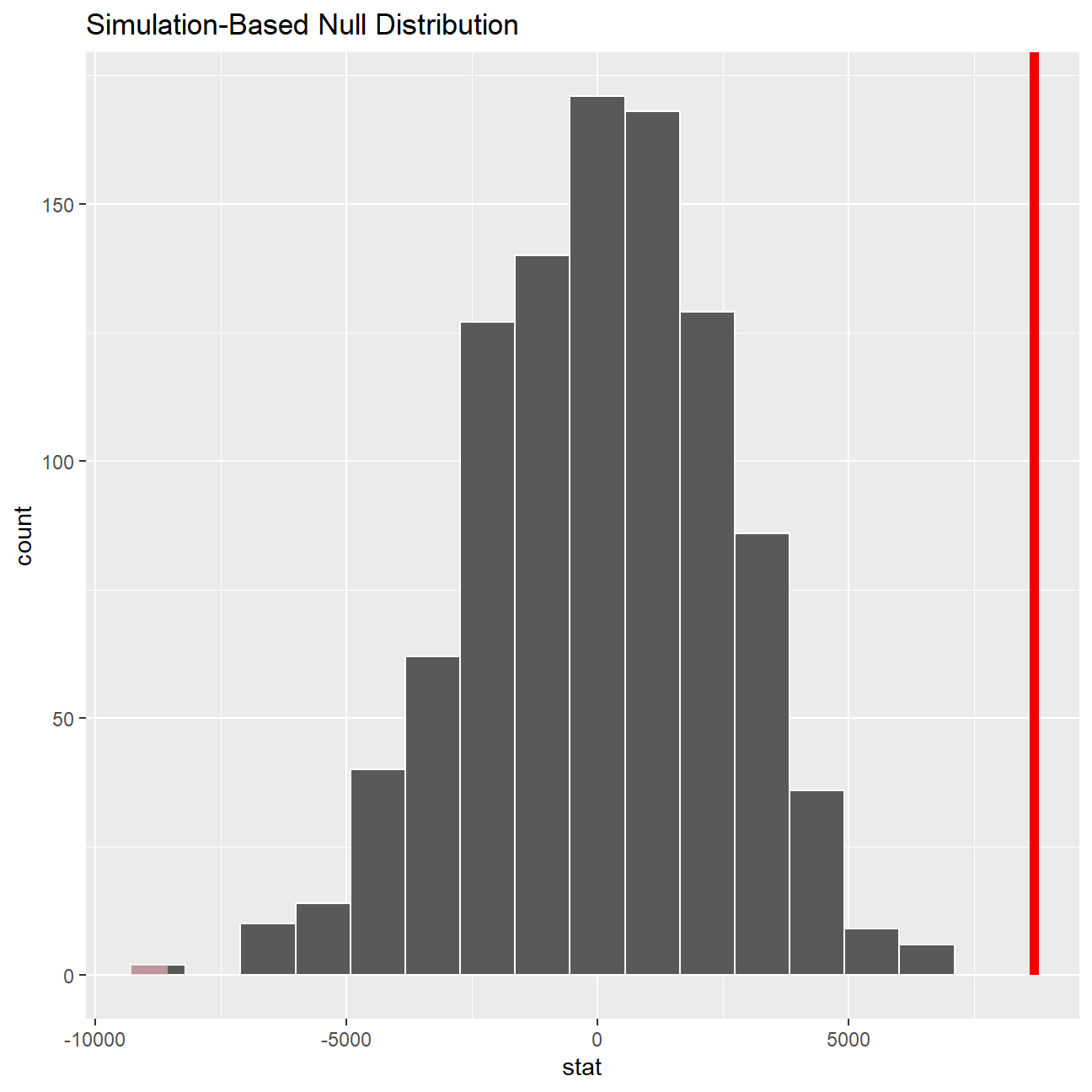

#now getting p value for conclusion

p_value_by_gender<-salary_by_gender %>% 
  get_p_value(obs_stat = df_by_gender2[2,2]-df_by_gender2[1,2], direction = "both")
p_value_by_gender

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1       0

#p_value is tiny, so the null hypothesis can be rejected

Looking at the graph the x axis ends at 10,000 dollars. The difference in the mean values of the gender salaries is 8,696 dollars. We can see that this results in a p-value close enough to zero, so we can conclude that at a 5% significance level there is a meaningful difference between the mean salaries of men and women.

Relationship Experience - Gender?

At the board meeting, someone raised the issue that there was indeed a substantial difference between male and female salaries, but that this was attributable to other reasons such as differences in experience. A questionnaire send out to the 50 executives in the sample reveals that the average experience of the men is approximately 21 years, whereas the women only have about 7 years experience on average (see table below).

# Summary Statistics of salary by gender
stats_exp_gender <- favstats (experience ~ gender, data=omega)

# Calculate 95% confidence intervals for experience by gender
exp_gender_ci <- omega %>% 
  group_by(gender) %>%
  summarise(mean_exp = mean(experience),
            sd_exp = sd(experience),
            count = n(),
            t_critical = qt(0.975, count -1),
            se_exp = sd_exp/sqrt(count),
            margin_of_error_exp = t_critical * se_exp,
            exp_low = mean_exp - margin_of_error_exp,
            exp_high = mean_exp + margin_of_error_exp)

exp_gender_ci

## # A tibble: 2 x 9
##   gender mean_exp sd_exp count t_critical se_exp margin_of_error~ exp_low
##   <chr>     <dbl>  <dbl> <int>      <dbl>  <dbl>            <dbl>   <dbl>
## 1 female     7.38   8.51    26       2.06   1.67             3.44    3.95
## 2 male      21.1   10.9     24       2.07   2.23             4.61   16.5 
## # ... with 1 more variable: exp_high <dbl>

# We can see that the confidence intervals for men and women in regards to experience do not overlap. This would allow us to reject the null hypothesis, but we will carry out hypothesis testing anyway.

#t-test
t.test(experience~gender, data=omega, var.equal = FALSE)

## 
##  Welch Two Sample t-test
## 
## data:  experience by gender
## t = -5, df = 43, p-value = 1e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -19.35  -8.13
## sample estimates:
## mean in group female   mean in group male 
##                 7.38                21.12

#the t-test shows that we can accept the alternative hypothesis, there is a significant difference in means of experience by gender. We get a tiny p-value reported at 1e-05, so almost zero

# permutation test
set.seed(1234)
 
  experience_in_null <- omega %>%
    specify(experience ~ gender) %>%
    hypothesize(null = "independence") %>%
    generate(reps = 1000, type = "permute") %>%
    calculate(stat = "diff in means",
              order = c("female", "male"))
  
  experience_in_null %>% visualize() + shade_p_value(obs_stat = exp_gender_ci[2,2]-exp_gender_ci[1,2], direction = "both")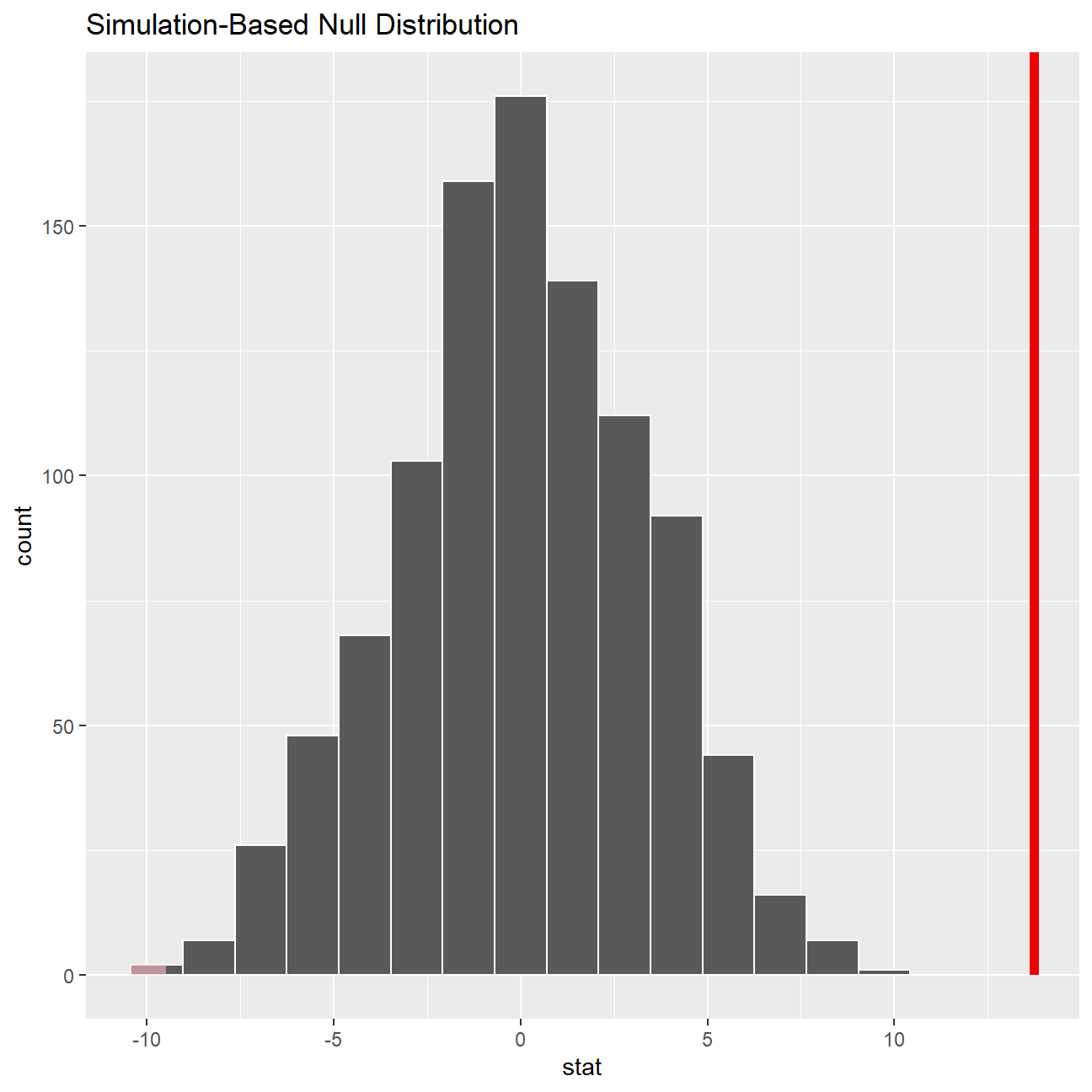

#now getting p value for conclusion

p_value_exp_gender <- experience_in_null %>% 
  get_p_value(obs_stat = exp_gender_ci[2,2]-exp_gender_ci[1,2], direction = "both")
               
p_value_exp_gender

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1       0

The person who raised the issue at the board meeting was correct in assuming that there is a statistically significant difference between the mean levels of experience for males and females in the company.

Relationship Salary - Experience ?

Someone at the meeting argues that clearly, a more thorough analysis of the relationship between salary and experience is required before any conclusion can be drawn about whether there is any gender-based salary discrimination in the company.

Analyse the relationship between salary and experience. Draw a scatterplot to visually inspect the data.

#We will draw a scatterplot to visually inspect relationship between salary and experience

  ggplot(omega,aes(x=experience,y=salary, colour= gender,fill=gender)) +
  geom_point() +
  geom_smooth(method = 'lm') +
  labs(title = "Women Make More Money per Year of Experience", x="Years of experience", y= "Salary") +
  theme_bw()+
  theme(legend.position = "none")+
  scale_y_continuous(labels= scales::dollar)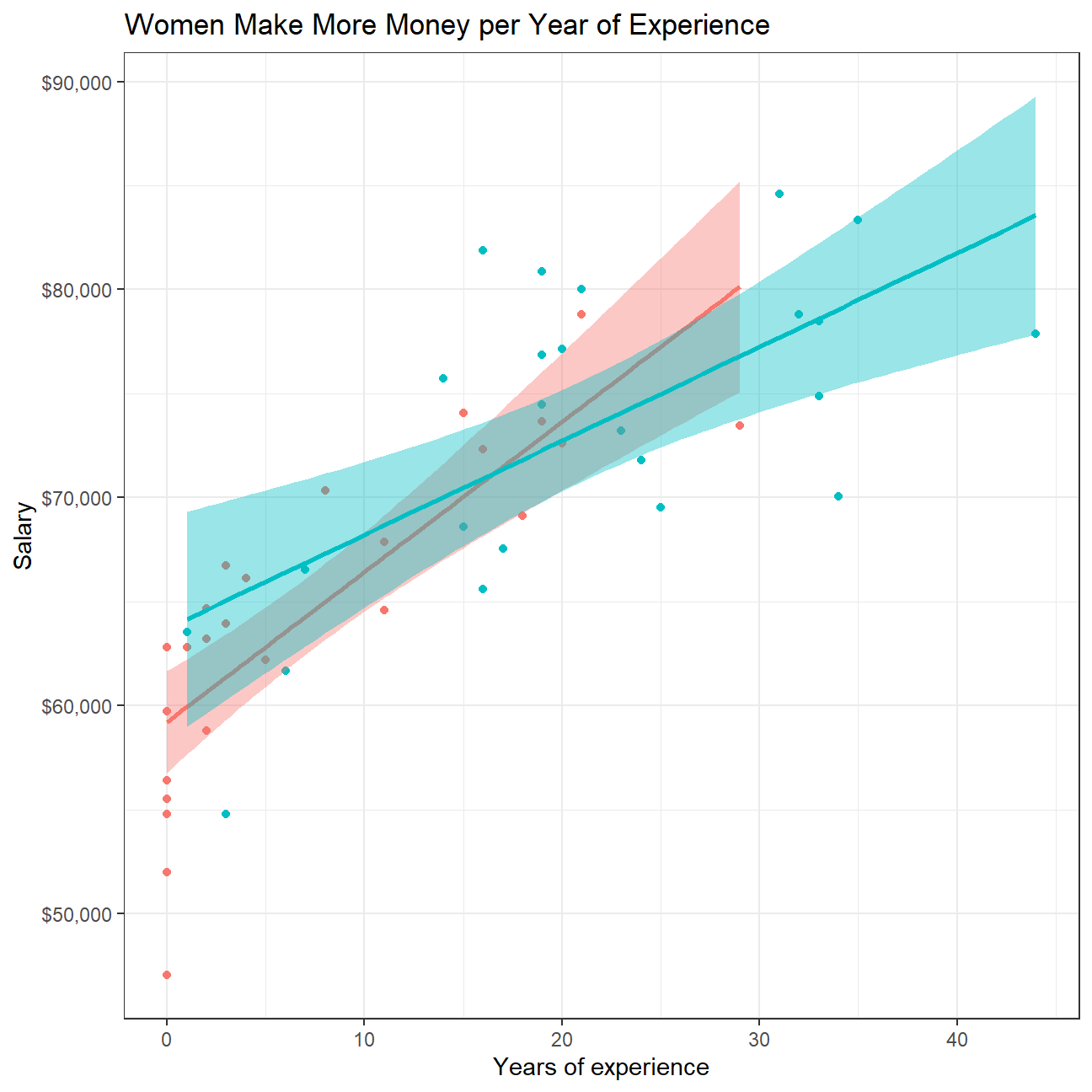

#We can observe a strong relationship between salary and experience. Increase in salary comes quickly at the beginning throughout first ~15 years, however the gains in salary become slower later over time.

As our analysis above shows, there is a significant positive relationship between years of experience and salary. We can also see what was confirmed in the previous section, that women have significantly less experience than men, with a cut off point displayed above at around 30 years. This gives an alternative reasoning besides discrimination regarding the pay gap, as more years of experience are a valuable asset that is accordingly financially rewarded with a greater salary.

Check correlations between the data

You can use GGally:ggpairs() to create a scatterplot and correlation matrix. Essentially, we change the order our variables will appear in and have the dependent variable (Y), salary, as last in our list. We then pipe the dataframe to ggpairs() with aes arguments to colour by gender and make ths plots somewhat transparent (alpha = 0.3).

omega %>% 
  select(gender, experience, salary) %>% #order variables they will appear in ggpairs()
  ggpairs(aes(colour=gender, alpha = 0.3))+
  theme_bw()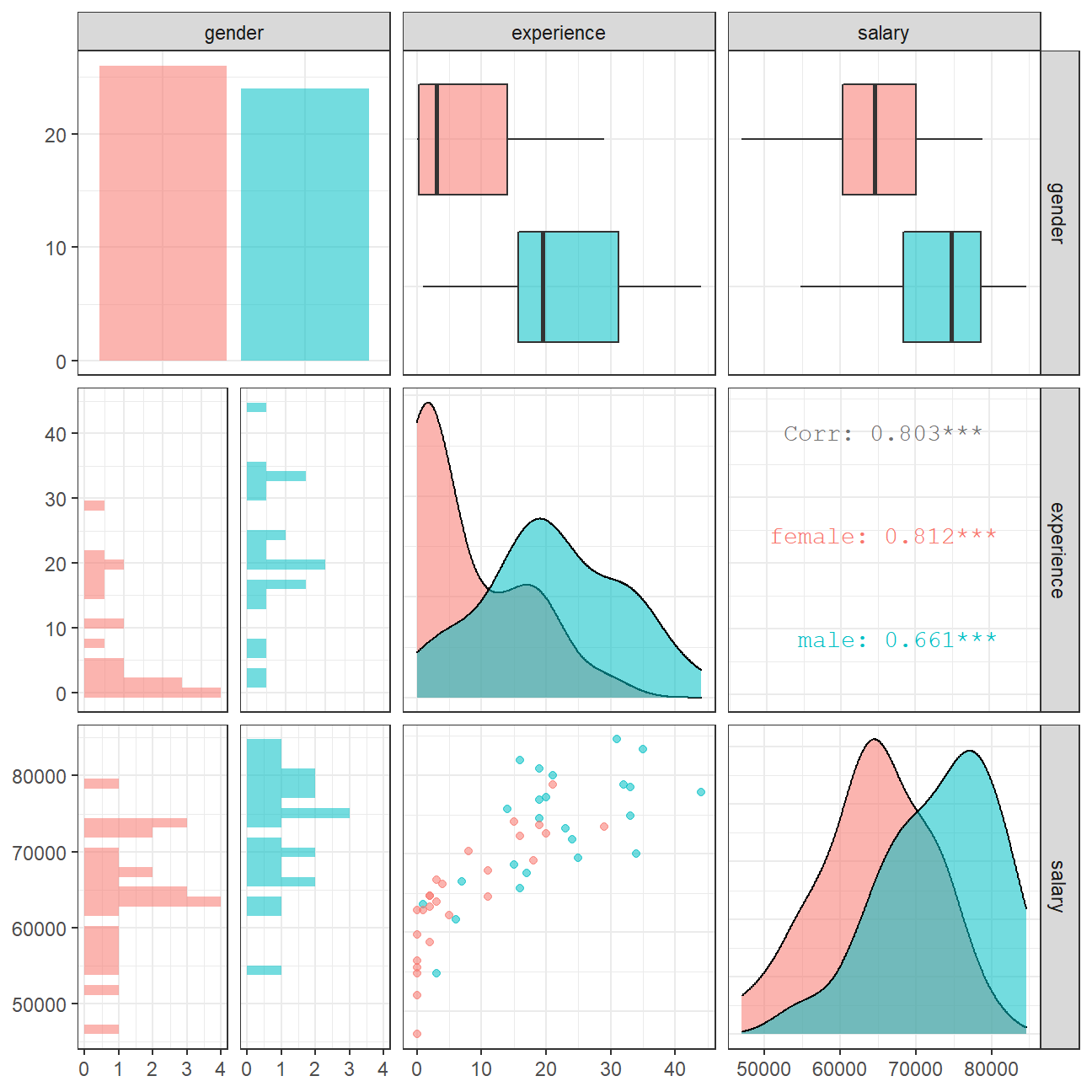

From the scatterplot we can see that the majority of women in the sample have a comparable salary to men with the same experience level.

The majority of women in the sample have experience between 0 and 20 years, whereas the approximate range of experience for most men is between 10 and 35 years. We also saw above that there is a statistically significant difference between the levels of experience for both genders, which confirms what we are seeing. Women seem to end their careers earlier, at least within the given sample.